Giải đề thi tuyển sinh 10 môn toán chuyên sở GD&ĐT Hải Dương p4

Giải đề thi tuyển sinh 10 môn toán chuyên sở GD&ĐT Hải Dương p4

Câu 4:

1. Cho tam giác đều ABC nội tiếp đường tròn (O), điểm E thuộc cung nhỏ AB của đường tròn \(\left( O \right)\,\,\left( {E \ne A,\,E \ne B} \right)\). Đường thẳng AE cắt các tiếp tuyến tại B,C của đường tròn (O) lần lượt tại M,N

a, Chứng minh rằng \(MB.NC = A{B^2}\)

b, Gọi F  là giao điểm của  MC và BN , H  là trung điểm. Chứng minh rằng ba điểm E,F,H  thẳng hàng.

2. Cho đường tròn (O) và hai điểm A,B cố định nằm trên đường tròn (O) sao cho \( \widehat {AOB} = {120^0}\). Điểm M thay đổi trên cung lớn AB của đường tròn (O). Đường tròn nội tiếp tam giác MAB tiếp xúc với MA,MB lần lượt tại E,F .Chứng minh rằng đường thẳng EF luôn tiếp xúc với một đường tròn cố định.

1,

a,

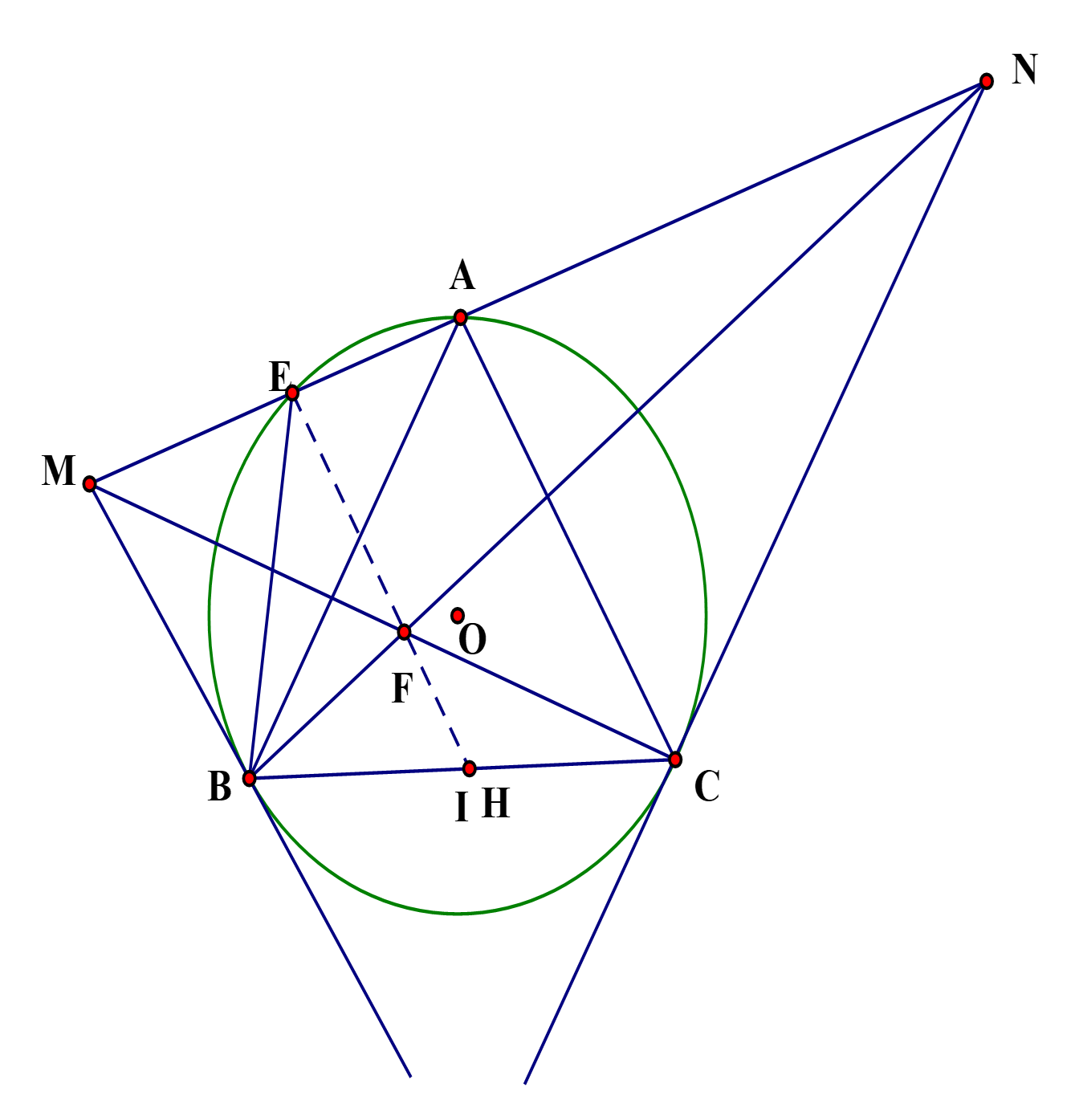
Chứng minh rằng:  \(MB.NC = A{B^2}\)

Ta có: \(\widehat {ABM} = \widehat {ACB} = \widehat {BAC} = {60^0} \Rightarrow BM//AC \Rightarrow \widehat {BMA} = \widehat {CAN}\,\,\left( 1 \right)\)

Tương tự ta có:

\(CN//AB \Rightarrow \widehat {BAM} = \widehat {CNA}\,\,\left( 2 \right)% \)

Từ (1) và (2) ta có:

\(\Delta AMB\) đồng dạng \(\Delta NAC\) (g,g)

\(\Rightarrow \frac{{MB}}{{AC}} = \frac{{AB}}{{NC}} \Rightarrow MB.NC = AB.AC \Rightarrow MB.NC = A{B^2}\)

b, Gọi: F là giao điểm của\(MC\) và BN

H là trung điểm BC

Chứng minh 3 điểm E,F,H thẳng hàng

I là giao điểm của EF và BC

Từ a, suy ra \(MB.NC = B{C^2} \Rightarrow \frac{{MB}}{{BC}} = \frac{{BC}}{{NC}}\,\,\,\left( 3 \right)\)

Mặt khác \(\widehat {MBC} = \widehat {MBA} + \widehat {ABC} = {60^0} + {60^0} = {120^0}\)

Tương tự:

\(\widehat {BCN} = {120^0}\)

Suy ra:

\(\widehat {MBC} = \widehat {BCN}\,\left( 4 \right)\)

Từ (3) và (4) ta có :

\(\Delta MBC\) đồng dạng\(\Delta BCN\) (cgc)

Suy ra:

\(\widehat {BMC} = \widehat {NBC}\)

Ta có:

\(\widehat {BFM} = \widehat {BCF} + \widehat {FBC} = \widehat {BCF} + \widehat {BMC} = {180^0} - \widehat {MBC} = {60^0}\,\left( 5 \right)\)

Do \(BEAC\) nội tiếp nên \($\widehat {BEM} = \widehat {BCA} = {60^0}\,\,\left( 6 \right)\)

Từ (5) và (6) ta có \(\widehat {BFM} = \widehat {BEM}\)

Suy ra:

\(BMEF\) nội tiếp

\(\Delta IBF\) đồng dạng \(\Delta IEB\) (g.g)

\(\frac{{IB}}{{IE}} = \frac{{IF}}{{IB}} \Rightarrow I{B^2} = IE.IF\,\,\left( 7 \right)\)

Chứng minh tương tự ta có:

\(I{C^2} = IE.IF\,\,\left( 8 \right)\)

Từ (7) và (8) suy ra \(IB = IC \Rightarrow I \equiv H\)

Vậy: \(E,\,F,\,H\) thẳng hàng

2. Cho đường tròn \(\left( O \right)\) và hai điểm \(A,\,B\) cố định nằm trên đường tròn \(\left( O \right)\) sao cho\(\widehat {AOB} = {120^0}\) Điểm M thay đổi trên cung lớn của đường tròn\(\left( O \right)\). Đường tròn nội tiếp tam giác MAB tiếp xúc với\(MA,\,MB\) lần lượt tại E và F. Chứng minh rằng đường thẳng EF luôn tiếp xúc với một đường tròn cố định

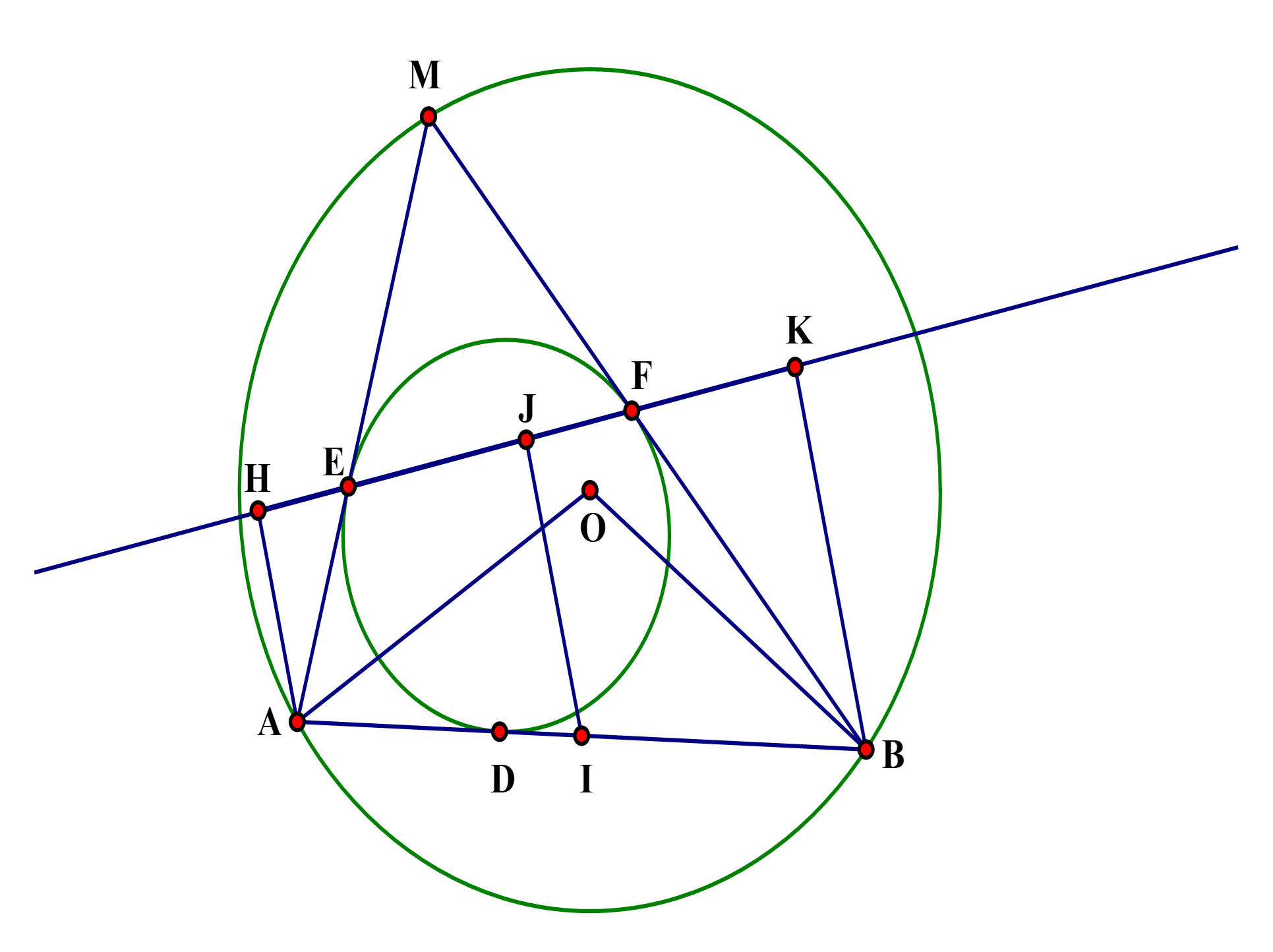
Gọi I là trung điểm AB

vẽ \(AH,\,IJ,\,BK\) cùng vuông góc với EF

Ta có:

\(\widehat {AOB} = {120^0} \Rightarrow \widehat {AMB} = {60^0}\)

Hơn nữa: \(ME = \,MF\)

nên tam giác \(MEF \) đều

Tam giác vuông \(AHE\) có \(AH = AE.\sin \,{60^0} = \frac{{\sqrt 3 }}{2}.AE = \frac{{\sqrt 3 }}{2}.AD\,\,\,\left( 1 \right)\)

Tam giác vuông BKF có \(BK = BF.\sin \,{60^0} = \frac{{\sqrt 3 }}{2}BF = \frac{{\sqrt 3 }}{2}BD\,\,\left( 2 \right)\)

Cộng vế (1) và (2) ta có \(AH + BK = \frac{{\sqrt 3 }}{2}AB \Rightarrow 2IJ = \frac{{\sqrt 3 }}{2}AB \Rightarrow IJ = \frac{{\sqrt 3 }}{4}AB\)

Vì điểm I cố định nên:

EF tiếp xúc với đường tròn cố định tâm I có bán kính  \(\frac{{\sqrt 3 }}{4}AB\)

Hết phần 4

Tìm kiếm tài liệu học tập về chuyên đề, đề thi thử ôn thi vào 10 môn Toán

chuyên đề tam giác, các dạng bài tập về đường tròn, chứng minh tiếp xúc đường tròn ....

tất cả đều có tại https://tailieuthi.net/